Tag: Matematica

Sto leggendo un po’ di cose sulla probabilità bayesiana.
È un tema interessante – oserei dire persino: importante – che non riguarda solo la matematica ma in generale il modo in cui ragioniamo e quello che potremmo chiamare “scetticismo sensato”.

Ma restiamo sulle probabilità bayesiane.
Di risorse in italiano ne ho trovate poche; in inglese c’è un bel video introduttivo di 3Blue1Brown e due libri: il primo è un’introduzione con diversi esempi e metodi (Bayes’ Theorem Examples: A Visual Introduction For Beginners di Dan Morris), il secondo è una interessante storia del teorema e delle sue alterne fortune nella storia (The Theory That Would Not Die di Sharon Bertsch McGrayne).

La mente bayesiana

Una cosa che mi ha colpito è un’apparente contraddizione.

Di per sé il teorema di Bayes spiega come dovremmo aggiornare una credenza iniziale alla luce di nuove informazioni. Credo che le chiavi di casa siano nella tasca del cappotto e non nello zaino; infilo la mano nella tasca del cappotto e non le trovo; correggo la mia ipotesi iniziale e penso che siano nello zaino; non le trovo neanche lì e allora penso di non aver controllato bene in tasca; solo alla fine concludo di aver verosimilmente perso le chiavi.

È normale ragionare così. Vero che non facciamo valutazioni numeriche tipo “al 90% le chiavi sono in tasca” (o “sono pronto a scommettere 1 a 9 che le chiavi sono in tasca”), “il 5% delle volte che non trovo le chiavi è perché non le ho cercate bene” (o “sono pronto a scommettere 1 a 19 che non sono lì visto che non le ho trovate”), “le probabilità di perdere le chiavi sono inferiori all’1%” (o “sono pronto a scommettere 1 a 99 che non le ho perse”) e non ci mettiamo a fare i calcoli che poi ho riassunto alla fine di questo articolo, ma tutti noi facciamo un secondo controllo in tasca prima di convincerci che potremmo aver perso le chiavi.

Secondo vari studi, citati nell’ultimo capitolo del saggio di Sharon Bertsch McGrayne, la nostra mente è bayesiana: riduce in continuazione l’incertezza grazie a nuove osservazioni.

Eppure il teorema di Bayes porta spesso a risultati controintuitivi, spesso presentati come dei paradossi. Quello più famoso riguarda la probabilità di avere una malattia relativamente poco diffusa (diciamo una persona su mille) se un test diagnostico affidabile al 99% risulta positivo (e non abbiamo altri motivi di sospettare di essere malati, ovviamente).

Un altro riguarda un indovinello apparso su questo sito una decina di anni fa:

Una cassa contiene diecimila monete. Una di queste è truccata, e lanciandola in aria esce sempre testa, mentre tutte le altre sono normali, con eguali probabilità per testa e croce.
Prendo una moneta a caso e la lancio otto volte, ottenendo sempre testa.
È ragionevole concludere che abbia trovato la moneta truccata? Più in generale, dopo quanti lanci è ragionevole pensare di avere in mano la moneta truccata?

Intuitivamente pensiamo che il risultato positivo di un test così affidabile equivalga a una diagnosi quasi certa e che otto teste di fila siano possibili solo con una moneta truccata. Ma solo in un caso su dieci chi ha ricevuto un test positivo è ammalato. Nel caso delle monete, invece, con otto lanci c’è un misero 2,5% di probabilità di aver preso la moneta truccata.

Come è possibile che questi risultati ci sorprendano se la nostra mente è bayesiana?

Una prima risposta è che un conto è rivedere le nostre ipotesi iniziali, un altro è farlo correttamente. Il ragionamento in entrambi i casi è infatti corretto: è vero che il test positivo aumenta la probabilità di essere malati, è vero che ottenere otto volte testa aumenta le probabilità di aver preso la moneta truccata, ma non così tanto da farci cambiare l’ipotesi iniziale. Un secondo test risultato positivo, o qualche altra testa ottenuta lanciando la moneta, e avremmo valide ragioni per cambiare idea.

Tuttavia sospetto che possa esserci anche un altro problema. La formulazione del problema ci porta a trascurare le probabilità iniziali. Pensiamo che o siamo sani o siamo malati, che la moneta che abbiamo in mano o è truccata o è normale. Ma se partiamo dal fatto che c’è una probabilità su mille di essere malati, è abbastanza scontato che un test che sbaglia in un caso su cento non ci darà alcuna certezza (ma certamente ridurrà l’incertezza che infatti passa dallo 0.1% al 10%). E se pensiamo che avevo una possibilità su diecimila di aver preso la moneta truccata, l’aver ottenuto otto volte testa è insolito – ci sono altre 255 possibilità – ma non così determinante.

Siamo bayesiani quando non troviamo le chiavi in tasca; ci dimentichiamo di esserlo quando abbiamo test affidabili al 99% o monete truccate. E qui interviene un sistema di calcolo che ho trovato nel libro di Dan Morris e che potrebbe essere utile a orientarsi.

Il diagramma ad albero

L’idea è realizzare uno schema ad albero di quello che potrebbe accade, indicando per ogni ramo quante volte può capitare (posso farlo come numero di casi o come probabilità).

Prendiamo il caso delle monete. Quello che faccio è prendere una delle diecimila monete dalla cassa e poi lanciarla ottenendo 8 volte testa.

Il primo passaggio sarà quindi “prendo una moneta”: in un caso sarà quella truccata, negli altri 9’999 sarà una normalissima moneta.

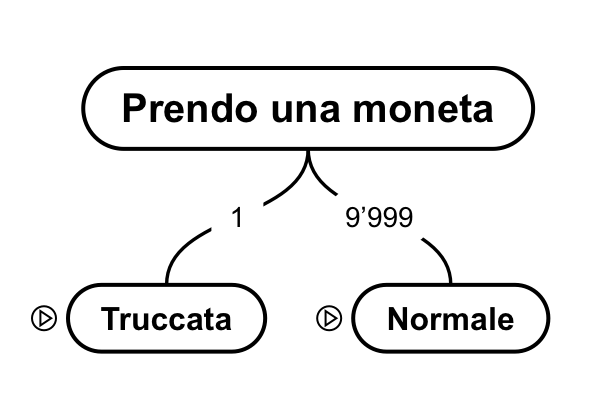
Il secondo passaggio sarà invece lanciare la moneta 8 volte. Se la moneta è truccata, non posso che ottenere 8 volte testa. Se ho preso una moneta normale, ci sono 256 possibili sequenze, ognuna delle quali ha circa 39 possibilità su 9’999.

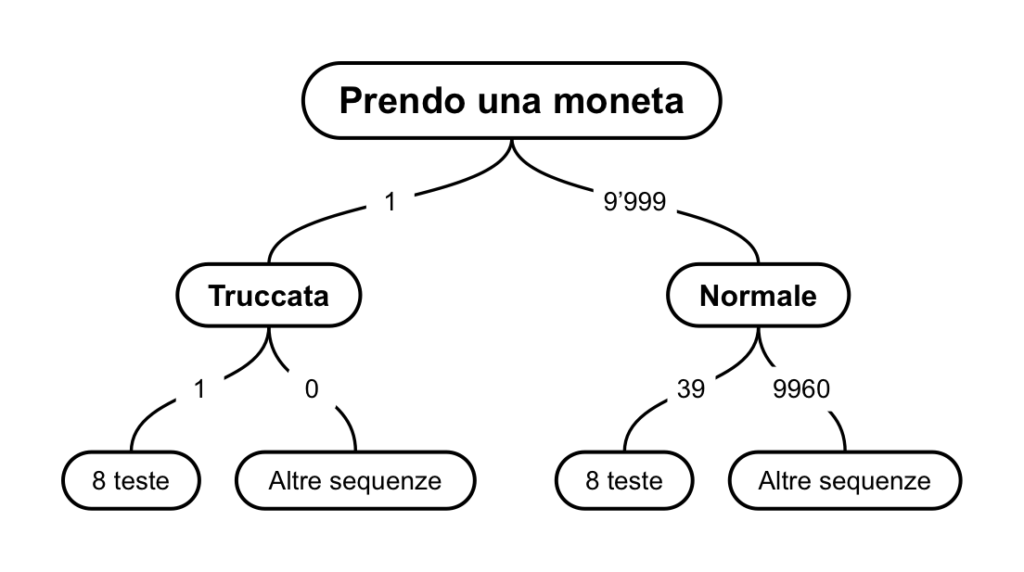
Una volta tracciato lo schema completo, cancello quello che non mi serve. So di aver ottenuto 8 volte testa, ma non so se con una moneta truccata o normale: posso quindi ignorare i rami in cui ho ottenuto altre sequenze e concentrarmi solo sui due che prevedono 8 teste.

Ho 40 scenari, in uno ho la moneta truccata, negli altri 39 una normale.

Il calcolo che mi ritrovo a fare è lo stesso previsto dal teorema di Bayes, ma senza dovermi ricordare la formula o calcolare le probabilità condizionali.

Per i test diagnostici ho realizzato lo schema mettendo nei rami le probabilità come frazioni e calcolando i totali a parte.

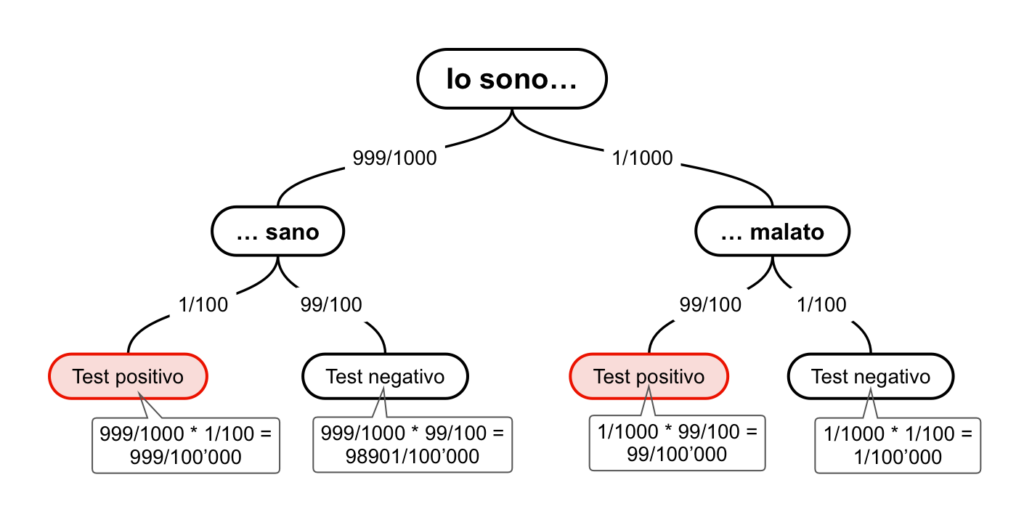
La probabilità a posteriori di essere malati se il test è risultato positivo è di 99/(999+99)=9%.

Il bello di questo schema è che permette di calcolare anche altre probabilità a posteriori; se ad esempio sono paranoico mi rincuorerà sapere che mentre un test positivo mi lascia sostanzialmente nell’incertezza, un test negativo è invece rassicurante: le probabilità di essere malati nonostante un test negativo sono infatti dello 0.001% (1/98’902).

Posso anche facilmente aggiornare i numeri: mettiamo che, avendo qualche sintomo, la stima iniziale di essere malato passi da una su mille a una su venti. In questo caso il test positivo mi dà una sicurezza di oltre l’80% di essere malato.

Il teorema di Bayes e le chiavi

Per un confronto, vediamo di applicare il teorema di Bayes al caso delle chiavi.

Ricapitolando: sono abbastanza sicuro (al 90%) di avere le chiavi in tasca; possibilista sul fatto che potrebbero invece essere nello zaino (9%) scettico sul fatto di averle perse (1%).
Se le chiavi non sono in tasca sono ovviamente certo (probabilità del 100%) di non trovarle; ma se ci sono ho comunque un 5% di probabilità di non trovarle.

Mettiamo il tutto in formule. La probabilità di avere le chiavi in tasca è , quella di averle nello zaino è e di averle perse è .
La probabilità di non rinvenirle in tasca (o nello zaino) è (rispettivamente ).
Infine, la probabilità condizionale è indicata con una barra verticale |. Quindi indica la probabilità di non trovare le chiavi in tasca sapendo che sono lì mentre è la probabilità che le chiavi siano in tasca sapendo di non averle trovate.

Ecco quindi le probabilità iniziali (in notazione decimale: 1=100%).

La probabilità di non rinvenire le chiavi in tasca se sono nello zaino (e viceversa) oppure se sono andate perse è banalmente 1.

Ecco adesso il teorema di Bayes:

Proviamo a calcolare la probabilità a posteriori che le chiavi siano in tasca sapendo che non le ho trovate:

Come calcolo , la probabilità di non trovarle in tasca?
È sufficiente sommare la probabilità che siano nello zaino o perse – e in questi casi è certo che non le troverò in tasca – con la probabilità che siano in tasca e non le ho trovate:

Quindi le probabilità a posteriori che le chiavi siano in tasca, nello zaino o perse:

In altre parole: se non trovo le chiavi in tasca, la probabilità che siano in tasca scende a circa il 30%, quella che siano nello zaino sale a circa il 60% mentre c’è un 7% di probabilità di averle perse.

Cosa succede se adesso le cerco nello zaino e non le trovo?
Le probabilità che ho appena calcolato diventano le mie nuove probabilità a priori dalle quali ripartire per fare i calcoli.

La possibilità di aver perso le chiavi è sempre più consistente (17%), ma è ancora più probabile che non abbiamo guardato bene in tasca.
Cosa succede, quindi, se faccio una seconda, infruttuosa ricerca delle chiavi in tasca?

.

La probabilità di aver perso le chiavi è ormai del 60% e (vi risparmio i calcoli) arriva a superare l'80% se faccio un'altra infruttuosa ricerca in borsa.